2.2. Экспериментальные подтверждения гипотезы де
Бройля
Критерием истинности любой
физической теории, любой гипотезы всегда является эксперимент.
Необходимость экспериментальной проверки гипотезы де Бройля была тем
более актуальна, что, во-первых, эта гипотеза касалась глубинных,
фундаментальных свойств материи, а во-вторых, наличие у частиц
волновых свойств не соответствовало традиционным представлениям
классической физики.
Первые
экспериментальные исследования, подтвердившие волновую природу
частиц, были выполнены американскими физиками К.
Дэвиссоном и Л. Джермером, а также
независимо английским физиком Дж. П.
Томсоном в 1927г. В этих работах использовалась дифракция
электронов на кристаллической решетке. Прежде чем перейти к
подробному описанию этих экспериментов, отметим следующее. Как уже
обсуждалось выше, дебройлевская длина волны электрона при не очень
большом значении ускоряющей разности потенциалов (~100 В) по порядку
величины составляет 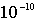 м.
Этот же порядок величины характерен для расстояния между атомными
плоскостями в кристалле. Поэтому, так же, как и в случае
рентгеновских лучей, кристалл может играть роль дифракционной
решетки для электронных волн.
Рассмотрим дифракцию электронов на совершенном кристалле,
т.е. кристалле, обладающем идеальной, без каких-либо нарушений
кристаллической решеткой. Электроны с дебройлевской длиной волны
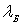
могут дифрагировать на различных атомных плоскостях (рис.2.1а),
выбор которых осуществляется взаимной ориентацией падающего пучка
электронов и рассеивающего кристалла. Пусть электроны падают на
кристалл под углом скольжения 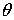
по отношению к рассеивающему семейству плоскостей. Для простоты
рассмотрим симметричный случай (рис.2.1б), когда поверхность
кристалла 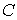
параллельна рассеивающим плоскостям, хотя на практике это условие
далеко не всегда выполняется. Тогда угол 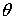
будет углом скольжения, под которым электроны падают на поверхность
кристалла, а угол 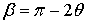
- углом между падающим и дифрагировавшим пучками электронов.
Теоретический анализ
дифракции электронов на кристаллах во многом аналогичен случаю
рентгеновских лучей. При значении угла 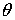 ,
удовлетворяющем условию Брэгга-Вульфа
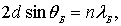 |
(2.10) |
возникает интенсивный
дифракционный максимум отраженной волны. Здесь 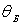
- брэгговский угол, 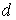
- расстояние между отражающими плоскостями (постоянная решетки
кристалла), 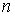 -
целое число, принимающее значения 1, 2, 3, ... , называемое порядком
отражения.
Физический смысл условия
Брэгга-Вульфа (2.10)
достаточно прозрачен: дифракционный максимум появляется в тех
случаях, когда разность хода волн, отраженных от соседних атомных
плоскостей, равна целому числу длин волн де Бройля. Именно в этом
случае отраженные волны усиливают друг друга, т.е. имеет место
конструктивная интерференция.
Отметим,
что условие (2.10)
получено без учета преломления электронных волн в кристалле. С
учетом преломления условие Брэгга-Вульфа принимает вид
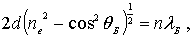 |
(2.11) |
где
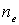
- показатель преломления электронных волн (см. задачу 2.3).
Опыт Дэвиссона и Джермера. Дэвиссон и Джермер
исследовали дифракцию электронов на монокристалле никеля,
кристаллическая структура которого была известна из опытов по
дифракции рентгеновских лучей. Схема их эксперимента представлена на
рис. 2.2. Электроны от электронной пушки 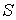 ,
прошедшие ускоряющую разность потенциалов 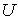 ,
падали нормально на сошлифованную поверхность кристалла никеля 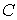 .
С помощью детектора 
исследовалось число электронов, отраженных от кристалла под углом
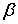
при различных значениях 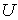 .
Напомним, что разным значениям 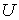 ,
согласно (2.8),
соответствуют разные дебройлевские длины волн электронов.
Кристаллическая решетка в
опыте Дэвиссона и Джермера играла роль объемной отражательной
дифракционной решетки, и с точки зрения гипотезы де Бройля
увеличение амплитуды отраженной волны при выполнении условия
Брэгга-Вульфа (2.10)
означало существенный рост вероятности отражения электронов, что и
приводило к наблюдаемому увеличению числа отраженных от кристалла
электронов.
Результаты
экспериментальных исследований Дэвиссона и Джермера представлены на
рис.2.3, где приведены полярные диаграммы интенсивности отраженных
электронов при нескольких значениях ускоряющей разности потенциалов
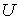 .
При 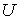
= 44 В (рис.2.3 а) дифракционный максимум под углом 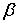
= 50 0 только начинает формироваться, при 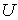
= 54 В (рис.2.3 в) он достигает максимальной интенсивности, а при
дальнейшем возрастании 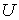
(рис.2.3 г, д) опять ослабляется вплоть до полного исчезновения.
|
|
|
Рис. 2.3.
Динамика дифракционного
отражения электронов при изменении ускоряющей разности
потенциалов U |
В
опытах Дэвиссона и Джермера максимальное отражение электронов
наблюдалось при ускоряющей разности потенциалов 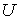 =
54 В , что соответствует дебройлевской длине волны
Длина
волны, определяемая из условия Брэгга-Вульфа (2.10)
для постоянной решетки никеля 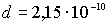 м
равнялась 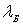
= 0,165 нм. Это совпадение экспериментальных и расчетных значений
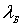
служит прекрасным подтверждением гипотезы де Бройля о наличии у
частиц волновых свойств.
Дэвиссоном и Джермером
была также измерена интенсивность дифрагировавших электронов при
фиксированном угле отражения 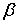
(постоянном угле скольжения 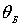 )
в зависимости от ускоряющей разности потенциалов 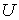 .
Результаты этого опыта приведены на рис. 2.4. Наблюдаемые на
эксперименте максимумы отражения отстоят друг от друга на равном по
шкале 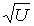
расстоянии, что подтверждается и в теории. Действительно, поскольку
то,
пользуясь условием Брэгга-Вульфа (2.10)
, получаем
где
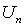
- ускоряющая разность потенциалов, отвечающая 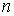 -му
порядку отражения, а 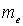
- масса электрона. Таким образом, связь между 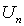
и 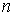
имеет вид
что и
свидетельствует об эквидистантности максимумов отражения в
зависимости от величины
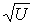 .
|
|
|
Рис. 2.4.
Зависимость интенсивности
пучка электронов, дифрагировавшего на монокристалле никеля, от
ускоряющего напряжения U при постоянном значении угла
тета. |
Различие теории и
эксперимента в этом опыте заключалось в том, что положения
дифракционных максимумов, наблюдаемых на эксперименте, не совпадали
с положениями максимумов, определяемых из условия Брэгга-Вульфа (2.10)
и показанных на рис.2.4 вертикальными стрелками. Особенно заметным
это различие было для небольших значений 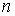 ,
т.е. для небольшой величины ускоряющей разности потенциалов 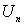 .
Причина такого расхождения теории и эксперимента состоит в том, что
условие Брэгга-Вульфа (2.10)
не учитывает преломление электронных волн в металле. Использование
условия (2.11)
полностью устраняет это расхождение.
Опыт Дж. П. Томсона. В экспериментах Томсона
исследовалась дифракция электронов на
поликристаллическом образце. Коллимированный пучок
моноэнергетических электронов падал нормально на тонкую
металлическую поликристаллическую фольгу (рис.2.5). На фотопластине,
|
|
|
Рис. 2.5.
Дифракция электронов на
поликристаллической фольге |
расположенной за фольгой,
прошедшие электроны образовывали дифракционную картину в виде тонких
концентрических колец. Поясним, почему при дифракции на
поликристаллическом образце на фотопластине получаются дифракционные
кольца.
Как
известно, поликристалл состоит из большого числа очень маленьких
монокристаллических зерен - кристаллитов, которые хаотически
ориентированы по отношению друг к другу. На рис. 2.6. а
параллельными линиями показана ориентация некоторой выделенной
системы атомных плоскостей в кристаллитах. Эта ориентация
произвольным образом меняется при переходе от одного кристаллита к
другому.
При
падении пучка электронов на поликристалл в нем всегда найдутся
кристаллиты, ориентированные так, что какая-либо система атомных
плоскостей будет находиться в отражающем положении, т.е. для нее
будет выполняться условие Брэгга-Вульфа (2.10)
Рассмотрим случай, когда
постоянная решетки 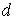
и порядок отражения 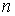
фиксированы, т.е. когда значение брэгговского угла 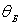
однозначно определено. Пусть пучок электронов падает под углом 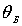
на систему атомных плоскостей кристаллита, представленную на рис.
2.6.б параллельными линиями. Легко видеть, что дифрагировавший пучок
электронов будет отклонен на угол 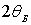
по отношению к проходящему пучку. Таким образом, дифракция на
отдельном кристаллите будет давать точку на фотопластинке.
|
|
|
Рис. 2.6a.
Дифракция в поликристалле
- структура поликристаллического образца
|
|
|
|
Рис. 2.6б.
Дифракция в поликристалле
- дифракционное отражение от отдельного кристаллита
|
Ввиду
осевой симметрии задачи вклад в дифракционное отражение будут также
давать кристаллиты, у которых рассматриваемые отражающие плоскости
повернуты относительно оси, задаваемой направлением падения
электронов, при условии, что падение осуществляется под тем же углом
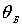 .
Следовательно, в случае поликристалла дифракционное отражение от
одного семейства плоскостей при фиксированном значении 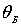
будет происходить в конус с углом раствора 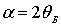
. Сечение этого конуса плоскостью фотопластинки дает окружность.
Вклад в отражение от разных плоскостей кристалла (разные значения
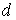 ),
а также учет различных порядков отражения 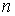
приводит к появлению на фотопластинке системы концентрических
окружностей.
В опыте
Томсона использовались быстрые электроны с энергией 17,5 - 56,5 кэВ,
поскольку медленные электроны интенсивно поглощаются фольгой, что
приводит к значительному ослаблению проходящего пучка. Результаты
эксперимента по дифракции электронов на поликристаллической фольге
представлены на рис.2.7.
|
|
|
Рис. 2.7.
Результаты дифракционных
опытов с электронами на поликристалле серебра
|
При
анализе дифракции электронов на поликристалле возник следующий
вопрос: можно было допустить, что дифракцию испытывают не электроны,
а вторичное рентгеновское излучение, испускаемое атомами кристалла
под действием электронного пучка. Для того чтобы однозначно
установить природу дифрагировавших частиц (электроны или
рентгеновские кванты), в области между фольгой и фотопластинкой было
создано магнитное поле. Если дифракцию испытывают электроны, то они
будут отклоняться магнитным полем, что приведет к искажению
дифракционной картины. Если же дифрагирует рентгеновское излучение,
то система колец должна остаться без изменений. Эксперимент с
магнитным полем показал, что дифракционное отражение испытывают
именно электроны.
Дифракция одиночных электронов. Рассмотренные выше
эксперименты проводились с достаточно интенсивными пучками частиц, в
данном случае электронов. Поэтому выявленные в них волновые свойства
могли быть приписаны как ансамблю взаимодействующих между собою
электронов, так и отдельному электрону. Для того, чтобы выяснить,
обладает ли индивидуальная частица волновыми свойствами, группа
отечественных физиков во главе с В.А.
Фабрикантом выполнила в 1949 г дифракционные исследования с
очень слабым пучком электронов. В этих опытах промежуток времени
между двумя последовательными прохождениями электронов через
кристалл в 30000 раз превышал время, затрачиваемое одним электроном
на прохождение всего прибора. Таким образом, электроны дифрагировали
в кристалле поодиночке и полностью исключалось взаимодействие
электронов друг с другом как причина возникновения дифракционной
картины. Качественный вид распределения дифрагировавших электронов
по фотопластинке приведен на рис. 2.8 . При небольшой длительности
эксперимента точки на фотопластинке, отвечающие попаданию
электронов, распределены совершенно случайным образом (рис.2.8а).
Однако при достаточной длительности эксперимента распределение точек
приобретает характерный для дифракции на поликристалле вид
концентрических колец (рис.2.8б). Таким образом было доказано, что
волновые свойства присущи отдельному электрону.
|
|
|
Рис. 2.8а.
Распределение
дифрагировавших электронов по фотопластинке - при небольшой
длительности эксперимента |
|
|
|
Рис. 2.8б.
Распределение
дифрагировавших электронов по фотопластинке - в случае
длительного эксперимента |
Опыты по дифракции без кристаллов. Первые опыты,
подтвердившие гипотезу де Бройля, были выполнены на кристаллах,
которые являются наиболее удобной дифракционной решеткой, созданной
природой для наблюдения дифракции электронных волн. В дальнейшем с
электронами был осуществлен ряд дифракционных опытов, аналогичных
тем классическим опытам, которые хорошо известны в оптике.
Наблюдалась дифракция электронов на крае полубесконечной плоскости,
на двух щелях и т.д. Были выполнены опыты по дифракции электронов в
неоднородном электрическом поле, которое играло роль аналога
бипризмы Френеля. Все эти эксперименты
подтвердили наличие у электронов волновых свойств.
Эффект Рамзауэра. В 1921 г немецкий физик К.Рамзауэр, исследуя упругое рассеяние электронов
на атомах аргона, обнаружил явление, которое не находило объяснения
в рамках классической физики. Лишь через несколько лет стало ясно,
что это явление представляет собой еще одно подтверждение волновых
свойств электрона и является электронным аналогом хорошо известного
в оптике пятна Пуассона.
Рамзауэр исследовал
поперечное сечение упругого рассеяния электронов 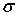
на атомах аргона при энергии электронов 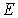
от долей электрон-вольта до нескольких десятков электрон-вольт.
Сечение упругого рассеяния электронов определяется выражением
где
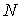
- число актов упругого рассеяния электронов на атомах аргона в
единицу времени, 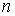
- плотность электронов в пучке, а 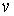
- их скорость. Сечение упругого рассеяния 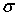
имеет размерность площади, оно представляет собой площадь мишени
вокруг атома, попадая в которую электрон испытывает упругое
рассеяние.
Сечение
упругого рассеяния зависит от энергии электронов 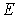
. Действительно, чем больше 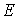
, тем больше скорость электрона 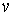
и тем меньше угол, на который отклоняется электрон при
взаимодействии с атомом при прочих равных условиях. Это означает,
что при уменьшении энергии (скорости) электронов сечение упругого
рассеяния должно увеличиваться.
Качественный вид
результатов измерения Рамзауэра приведен на рис.2.9. Для энергий
электронов, превышающих 16 эВ, сечение рассеяния 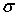
возрастает с уменьшением 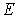
в соответствии с предсказаниями классической теории. Однако при
дальнейшем уменьшении 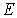
картина качественно меняется. При 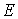
меньше 16 эВ сечение рассеяния убывает с уменьшением 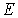
и при 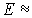
1 эВ 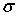
практически обращается в нуль. При дальнейшем уменьшении энергии
электронов сечение рассеяния вновь возрастает.
|
|
|
Рис. 2.9.
Качественная зависимость
сечения упругого рассеяния электронов на атомах аргона от
энергии электронов |
Обращение ![]()
в нуль означает, что атомы аргона становятся как бы прозрачными для
электронов, т.е. электрон проходит через атом аргона, не рассеиваясь
на нем. Этот экспериментальный результат, совершенно не совместимый
с представлениями классической физики, находит свое объяснение при
учете волновой природы электрона.
Из
оптики известно, что при дифракции на непрозрачном диске в центре
геометрической тени может существовать яркое пятно, называемое
пятном Пуассона. В опыте Рамзауэра роль такого диска играет атом
аргона. Если энергия электрона такова, что его дебройлевская длина
волны сравнима с диаметром атома, то в результате дифракции
электрона на атоме возникает пятно Пуассона для электронной волны.
Это означает, что электроны проходят через атом аргона, не испытывая
какого-либо отклонения от направления своего первоначального
движения. В дальнейшем подобное явление было обнаружено и для атомов
других инертных газов - криптона и ксенона. То обстоятельство, что
эффект Рамзауэра наблюдается только в инертных газах, объясняется
тем, что атомы инертных газов имеют полностью заполненную внешнюю
электронную оболочку, они сферически симметричны и обладают
достаточно резкой внешней границей.
Здесь
мы ограничились качественным анализом эффекта Рамзауэра. Решение
квантово-механической задачи о рассеянии электрона на атоме,
позволяющее получить определенные количественные соотношения,
приведено в разделе
4.4.
Опыты с нейтронами и пучками частиц. До сих пор,
обсуждая волновую природу микрочастиц, мы основное внимание уделяли
электрону. Это вполне естественно, поскольку первые эксперименты,
подтвердившие наличие у частиц волновых свойств, были выполнены
именно с электронами. Но согласно гипотезе де Бройля волновыми
свойствами должны обладать и другие микрочастицы - атомы, ионы,
молекулы, а также открытые позже электрона такие элементарные
частицы, как, например, протоны, нейтроны и т.д. Все эти частицы по
отношению к электрону являются тяжелыми частицами, так как их масса
значительно, в несколько тысяч раз, превосходит массу электрона.
Поскольку длина волны де Бройля 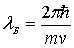
обратно пропорциональна массе частицы 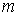 ,
то при одинаковых скоростях длина волны де Бройля тяжелых частиц
оказывается существенно меньше дебройлевской длины волны электрона.
Для того, чтобы наблюдать дифракцию тяжелых частиц на кристаллах,
необходимо, чтобы их дебройлевская длина волны была сравнима с
межплоскостным расстоянием в кристалле (~10 -10м), а это
оказывается возможным только в случае медленных частиц.
Дальнейшее
усовершенствование техники эксперимента позволило наблюдать
дифракцию на кристаллах тяжелых частиц, например, атомов гелия и
молекул водорода. Особенность этих опытов заключалась в том, что
дифрагировавшие атомы и молекулы из-за малой скорости не могли
проникнуть вглубь кристалла и испытывали дифракцию на двумерной
решетке, образованной атомами кристалла на его поверхности.
Большое
значение имело проведение дифракционных опытов с нейтронами. У
нейтронов нет электрического заряда и поэтому даже при малых
скоростях они могут свободно проникать в кристалл и дифрагировать на
трехмерной, пространственной кристаллической решетке. Источниками
нейтронов являются ядерные реакции, поэтому интенсивный пучок
нейтронов, необходимый для проведения дифракционных исследований,
может быть получен от ядерных реакторов или на ускорителях
заряженных частиц.
Анализ
показывает, что испытывать дифракцию в кристалле могут только так
называемые тепловые нейтроны, т.е. нейтроны,
энергия которых сравнима с энергией молекул газа 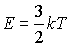
при комнатной температуре 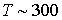
К. У тепловых нейтронов дебройлевская длина волны
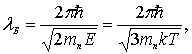 |
(2.12) |
где
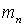 -
масса нейтрона, имеет порядок 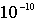
м , что делает возможным наблюдение дифракции нейтронов на
кристаллической решетке.
Первые
исследования, в которых наблюдалась дифракция
нейтронов на кристаллах, были выполнены в 1936 г Х. Хальбаном, П.
Прайсверком и Д. Митчеллом. В этих
экспериментах использовались радиево-бериллиевые источники
нейтронов, однако ниже мы приведем традиционную, сложившуюся за
последние десятилетия, схему эксперимента по дифракции нейтронов, в
которой источником нейтронов является ядерный реактор (рис.2.10).
|
|
|
Рис. 2.10.
Схема экспериментальной
установки для наблюдения дифракции нейтронов
|
Нейтроны от ядерного
реактора 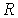
проходят через замедлитель 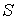
и теряют в нем часть своей энергии. Далее через коллимирующую
систему 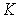 ,
формирующую узконаправленный пучок, они попадают на кристалл 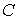 ,
в котором и происходит дифракция. Дифрагировавший пучок нейтронов
регистрируется детектором нейтронов 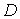 .
Характерный вид наблюдаемой на эксперименте зависимости
интенсивности дифрагировавших нейтронов от величины брэгговского
угла 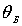
и дебройлевской длины волны 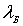
приведен на рис.2.11.
|
|
|
Рис. 2.11.
Дифракционный максимум
интенсивности нейтронов, отраженных от монокристалла
CsHSeO4 |
В
качестве замедлителя используются большие поликристаллические
образцы графита, бериллия, висмута и других веществ, ядра которых
слабо поглощают нейтроны. В замедлителе нейтроны испытывают
многократное дифракционное отражение и отдают избыток своей энергии
ядрам кристалла.
Кроме
того, в поликристаллическом замедлителе происходит выделение
низкоэнергетической части спектра нейтронного пучка ( фильтрация), также основанное на дифракции
нейтронов. Рассмотрим это явление подробнее.
следует, что максимальная
дебройлевская длина волны нейтронов, которые могут испытывать
дифракционное отражение, равна
Эту
длину волны 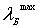
называют граничной длиной волны и обозначают ![]() .
Наличие граничной длины волны означает, что наиболее энергичные,
быстрые нейтроны с длиной волны ![]()
будут испытывать дифракцию в кристалле, отклоняться за счет этого от
своего первоначального направления и выбывать из проходящего пучка
(рис.2.12).
|
|
|
Рис. 2.12.
Схема фильтрации
нейтронного пучка поликристаллическим фильтром
|
Низкоэнергичные, медленные нейтроны с длиной волны 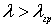
не испытывают дифракцию и проходят через поликристалл практически
без изменения интенсивности пучка. Наблюдавшаяся на эксперименте
зависимость интенсивности пучка нейтронов, прошедших через
поликристаллический бериллиевый фильтр, от дебройлевской длины волны
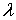
представлен на рис.2.13. Резкое уменьшение интенсивности прошедшего
пучка происходит при значении длины волны нейтронов 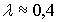 нм
, что согласуется со значением граничной длины волны для
бериллиевого фильтра 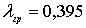
нм.
|
|
|
Рис. 2.13.
Спектр нейтронов,
прошедших через поликристаллический бериллиевый фильтр
|
Проходящие через
поликристаллический фильтр нейтроны низких энергий получили название
холодных нейтронов. Оценка температуры этих
нейтронов, выполненная в задаче 2.4, поясняет такое название.
Для
нейтронов, так же как и для других частиц, возможно
экспериментальное наблюдение классических дифракционных опытов,
хорошо известных в оптике. На рис. 2.14 приведены результаты
экспериментального исследования дифракции нейтронов на краю
непрозрачного экрана. В этом опыте использовались нейтроны с
дебройлевской длиной волны 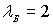 нм.
На графике одна единица по оси 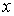
соответствует смещению приемной щели детектора шириной 30 мкм на
расстояние 100 мкм.
|
|
|
Рис. 2.14.
Интенсивность пучка
нейтронов, дифрагировавших на краю поглощающего экрана
|
Дифракционные опыты с
тяжелыми частицами - атомами, молекулами, нейтронами - показали, что
гипотеза де Бройля имеет универсальное значение. Все частицы,
независимо от их природы и внутреннего строения обладают волновыми
свойствами.
Задача
2.3. Получите условие Брэгга-Вульфа с учетом преломления электронной
волны в металле.
Решение:
Как было показано в разделе
2.1 , при падении электронов на поверхность металла происходит
преломление электронных волн де Бройля. Получим условие
Брэгга-Вульфа с учетом этого преломления.
Пусть
электроны падают на атомные плоскости кристалла под углом скольжения
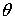 ,
угол скольжения для преломленной волны обозначим через 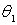
(рис.2.15) . Будем рассматривать симметричный случай, т.е. считать,
что атомные плоскости параллельны поверхности кристалла. Найдем
разность хода 
электронных волн, отраженных от соседних атомных плоскостей. С
учетом преломления получаем
|
|
|
Рис. 2.15.
Дифракция электронов с
учетом преломления электронной волны в металле
|
Закон
преломления (закон Снелиуса) для электронных волн имеет вид
Выражая
отсюда 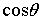
и подставляя его в выражение для разности хода  ,
получаем
Таким
образом, условие усиления волн, отраженных от соседних атомных
плоскостей, т.е. условие Брэгга-Вульфа, с учетом преломления
электронной волны де Бройля принимает вид (2.11)
Отметим,
что полученное условие Брэгга-Вульфа справедливо не только для
электронов, но и для других частиц, обладающих волновыми свойствами
- фотонов, нейтронов и т.д. Его использование оправдано в тех
случаях, когда показатель преломления 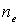
сколько-нибудь заметно отличается от единицы. Если же 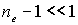
, то найденное условие переходит в условие Брэгга-Вульфа (2.10),
полученное без учета преломления.
Задача
2.4. Определите температуру 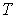 ,
соответствующую самым коротким волнам де Бройля нейтронов,
пропускаемых поликристаллом графита, постоянная решетки которого
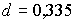
нм.
Решение:
Так как постоянная решетки графита 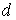
известна, то для граничной длины волны пропускаемых графитом
нейтронов (см. материал данного параграфа) получаем 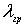 =
2 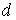 =
0,67 нм . Для того, чтобы найти температуру 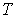 ,
соответствующую самым коротким волнам де Бройля пропускаемых
нейтронов, выразим из (2.12)
температуру 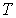
как функцию 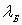
Подставляя сюда 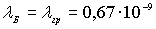 м
, находим, что
Таким
образом, мы видим, что нейтронам, прошедшим через
поликристаллический фильтр, действительно соответствуют очень низкие
температуры, так что их по праву называют холодными нейтронами.
|